Search

Two Groups, One Question: Is the Difference Significant?

Michael Lee, MBA
1 day ago
3 min read

The T-Test: How an Irish Brewer Revolutionized Statistical Analysis

Continuing Our Inferential Analysis Series

This article continues our deep dive into inferential analysis and hypothesis testing. In the previous pieces, we explored:

Now we turn our attention to the T-Test, used to compare the means between two groups.

The Story Behind the Test

The T-Test has an unexpected origin—it was developed in the early 1900s by William Sealy Gosset, a statistician working for Guinness Brewery in Dublin. The brewery needed to ensure quality across small batches of beer and couldn’t afford to test entire populations. Gosset created a new method—Student’s T-Test—for making confident decisions using small samples. Published under a pseudonym (to protect trade secrets), his work became a foundation of modern statistics.

What Is the Objective?

The T-Test helps us determine whether the average (mean) of two groups is significantly different. This is helpful for:

Comparing customer behavior across two promotions
Evaluating drug performance between two groups
Determining salary differences across departments
Assessing training effectiveness across delivery modes

Unlike Chi-Square (which compares categories), the T-Test works with numerical data.

When Should You Use a T-Test?

✅ Use this test when:

You are comparing two independent groups
Your outcome is numerical (like spending, time, or scores)
The data is approximately normal
The groups have similar variance (standard deviation)

🚫 Don't use this test if your variables are categorical or if you have more than two groups—use Chi-Square or ANOVA instead.

How It Works

Step 1: Define Hypotheses

Null Hypothesis (H₀): The means of the two groups are equal.
Alternative Hypothesis (H₁): The means of the two groups are different.

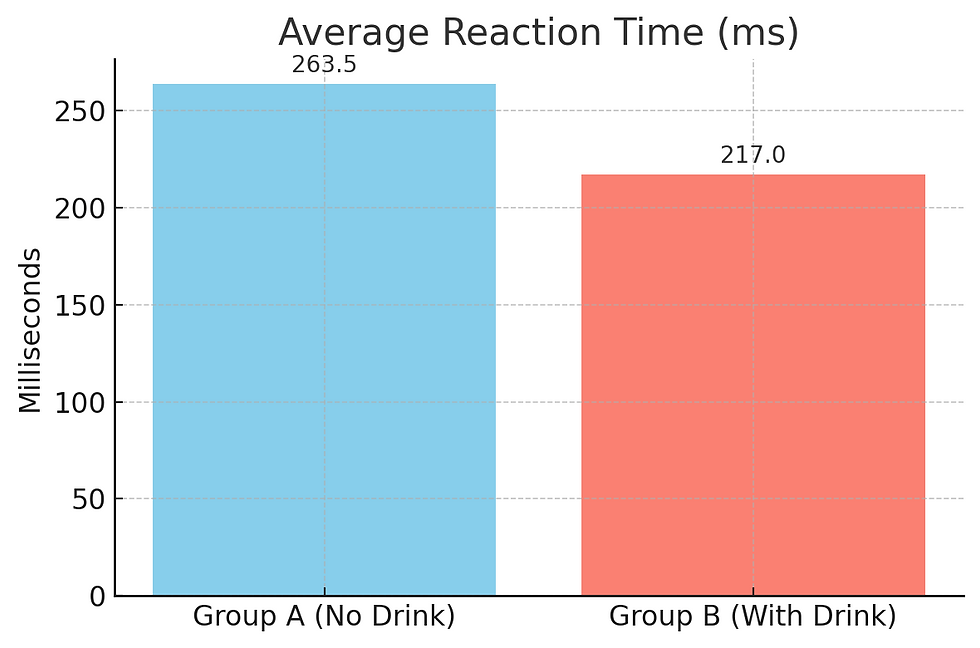
Example 1: Energy Drink and Reaction Time

We test whether a new energy drink improves reaction time:

Group A (Control): No drink
Group B (Test): Consumes the energy drink

Their reaction times (in milliseconds) are recorded:

Group A (No Drink)	Group B (With Drink)
250	230
270	210
260	215
255	220
275	225
280	235
265	210
250	200
270	220
260	215

Step 2: Calculate the T-Test Statistic

The formula is:

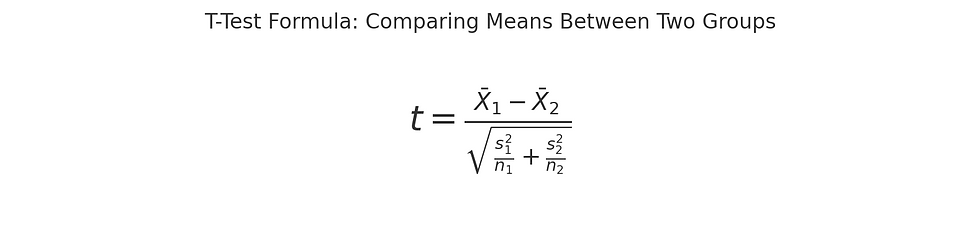
Where:

X̄₁, X̄₂ = Mean of each group
s₁², s₂² = Variance of each group
n₁, n₂ = Sample sizes (10 per group)

Step 2a: Compute the Means

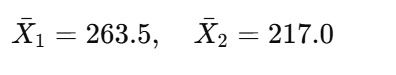
Step 2b: Compute the Variances

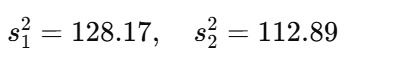
Step 2c: Compute the T-Statistic

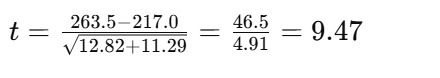
Step 3: Determine Statistical Significance

Degrees of freedom (df) = n₁ + n₂ – 2 = 18
Critical t-value at df = 18 and α = 0.05 (two-tailed) ≈ 2.101
Since t = 9.47 > 2.101, we reject the null hypothesis
p-value < 0.001: strong evidence that the means are different

✅ Result: The energy drink significantly improves reaction time. The improvement is unlikely due to chance.

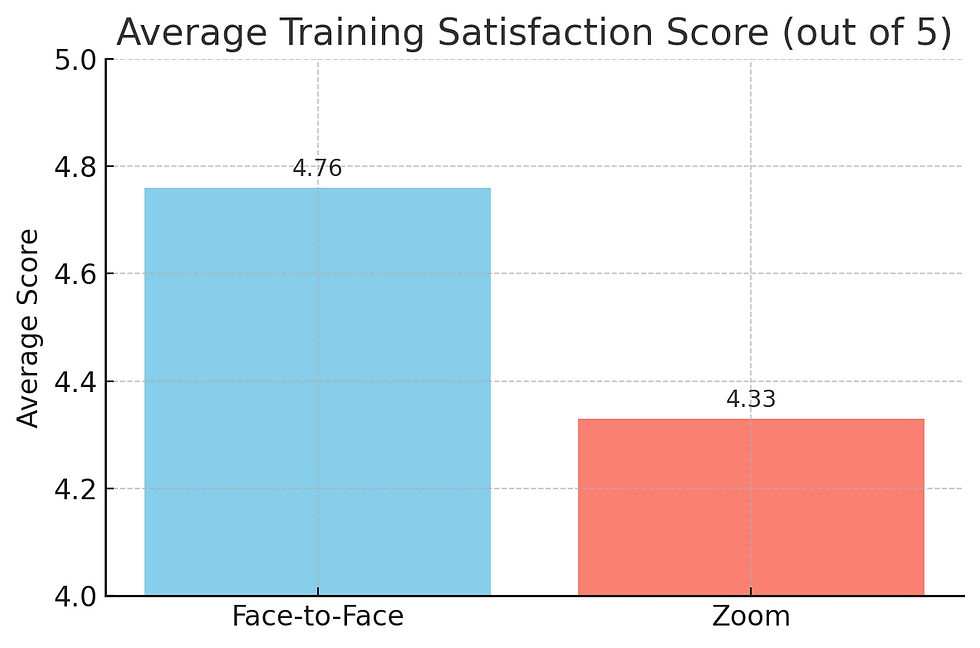
Example 2: Face-to-Face vs Zoom Training

You want to evaluate whether training delivery format affects participant satisfaction. After conducting the same training both face-to-face and over Zoom, you collect evaluation scores (out of 5) from each group.

Face-to-Face Scores	Zoom Scores
4.8	4.5
4.6	4.4
4.7	4.3
4.9	4.5
4.8	4.2
4.6	4.4
4.7	4.3
4.8	4.1
4.9	4.4
4.7	4.2

Average scores seem higher for face-to-face sessions. But is that difference meaningful or could it be random variation?

You run a T-Test and find:

t = 3.62, df = 18, p = 0.002
Since p < 0.05, the difference is statistically significant

✅ Result: Face-to-face training yields significantly higher satisfaction scores than Zoom. Trainers may want to consider hybrid strategies or boost engagement methods online.

Real-World Applications

1. Business & Pricing Strategies

Test whether discounted customers spend more than non-discounted ones.

2. Healthcare & Drug Testing

Compare patient outcomes under different treatments.

3. Education & Learning Methods

Evaluate different teaching methods or delivery formats—like face-to-face vs Zoom.

Final Thoughts

The T-Test is a must-have in your statistical toolkit. It’s easy to compute, practical, and powerful for answering the age-old question: “Is this difference real?”

If you want to gain hands-on experience with hypothesis testing and other powerful analytical techniques, our 2-day course, Problem Solving Using Data Analytics, provides practical applications and real-world exercises. For those curious about how Generative AI can enhance statistical testing, our Data Analytics in the Age of AI course explores AI-driven analytics and automation.